que es una funcion ?

estamos en presencia de una funcion cuando: 

NO estamos en presencia de una funcion cuando: 

 nota : y: f(x) 

Definicion de funciones polinomiales:

Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. El grado de un polinomio está dado por el mayor exponente de la variable en el polinomio, independientemente del orden en el que estén los términos

ejm:    f(x) = 3x⁵ − x² + 7x − 1     es una función polinomial de grado 5.

otra definicion:  

Si p(x) es un polinomio en la variable x entonces decimos que esta es una función polinomial p : R → R que asigna a cada punto x ∈ R el valor p(x) ∈ R.

funciones polinomicas basicas:

-funcion lineal:

 una funcion lineal es una funcione polinimica de primer grado; es decir, unafuncion  cuya representación en el plano carteciano es una linea recta. Esta función se puede escribir como:

f(x):mx+b

donde m y b son constantes reales

y  x es una variable real.

La constante m es la pendiente  de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

ejm:

Una función lineal de una única variable dependiente x es de la forma:  y:mx+b

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

y: 0.5x + 2 

en esta recta el parámetro m= 1/2 por tanto de pendiente  1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad;

 el valor de b es 2, luego la recta corta el eje y en el punto y= 2.

En la ecuación:

y: -x +5  

la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.

funcion cuadratica:   

o funcion de segundo grado es una funcion polinomica definida como:

 donde a, b y c son números reales cualquiera y a distinto de cero ya que si es cero nunca será una parábola. Este tipo de funciones tiene como característica que cuando a>0 el vértice  de la parábola se encuentra en la parte inferior de la misma y cuando a<0 el vértice se encuentra en la parte superior.

nota: la representacion grafica en el plano cartesiano de una funcion cuadratica es una parabola, cuyo eje de simetria es paralelo al eje d elas ordenadas.

-si el signo de a es positivo la parabola se abrira hacia arriba  y hacia abajo en el caso contrario   

La derivada de una función cuadrática es una función lineal y su integral una función cubica.

representaciòn  gràfica 

Corte con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

lo que resulta:

la función corta el eje y en el punto (0, c), siendo c el término independiente de la función.

A este punto de la función también se lo conoce con Ordenada al Origen, ya que se da en los términos

Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función

es decir:

las distintas soluciones de esta ecuacion de segundo grado, son los casos de corte con el eje x, que se obtienen, como es sabido, por la expresión:

.

Si la función no corta al eje x, la fórmula anterior no tiene solución (en los reales).

funciones racionales:

Una función racional es el cociente de dos funciones polinómicas. 

donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición  en el conjunto de todos los numeros reales menos los valores de x que anulen el denominador.Existe la posibilidad de encontrar valores de x tales que Q(x) sea igual a cero. Por este motivo las funciones racionales están definidas en todos los números que no anulan el polinomio denominador    

ejemplo: - Despeja y de la expresión xy = 1. ¿Qué tipo de función es?

respuesta:

Es una función racional que corresponde a una función de proporcionalidad inversa.

y = 1/x       Dom f(x)=R-{o}

- hallar el  dominio de la función

    4x-3/ x - 4

respuesta: dom f(x)= R-{4}

nota: (sabiendo que una asintota vertical se forma en los puntos donde la funcion no exite),las asintotas verticales  se dan mas que todo en  funciones racionales;  con la variable x en algún lugar del denominador. Cuando el denominador de una función racional se aproxima a cero, tiene una asíntota vertical.

ejemplo: 

 tu función es    y = 1/(x-2)    hallar el dominio  y la asintota vertical 

respuesta: 

debes resolver la ecuación   x-2 = 0, que es x = 2.    asintota vertical : x= 2  

dom f(x)= R-{2}

funciones irracioneles:

son aquellas cuya expresión matemática f(x) presenta un radical:

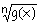
donde g(x) es una función polinómica o una función racional.

con g(x) como funcion racional

- si n de la raiz es impar, es posible calcular la imagen de cualquier numero real, siempre y cuand la expresion de g(x)  sea un      numero real, es decir  dom(f) es igual  dom(g)

-si n de la raiz es par, el radical esta definido para g(x) mayor o igual a 0 

ejemplo:

hallar el dominio, puntos de corte, tabla de valores  de la siguientefuncion irracional:

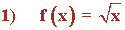
dominio: Como   n   es par, el dominio de   f(x)   es el conjunto de valores donde   x ≥ 0 , es decir,   Dom(f) = [0, +∞)

puntos de corte: f(0) = √0 = 0  ,  es decir, el punto de corte coincide con el eje de coordenadas   (0, 0).

tabla de valores: 

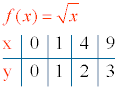
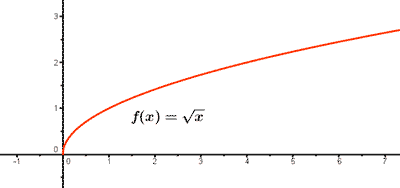
funciones pares e impares: 

pares

 una funcion f es par si para cualquier x del dominio se verifica  f(x) = f(-x)

en la siguiente funcion

observamos que para cualquier numero de x  y su opuesto -x tiene la misma imagen. En este caso decimos que la funcion es par.

nota: observamos que las funciones pares son simetricas respecto al eje vertical 

impares:    

una funcion f es impar si para cualquier x del dominio se verifica   f(x) = -f(-x)

consideramos ahora la funcion

Observamos que cualquier numero x  y su opuesto-x tienen imagenes opuestas. En este caso decimos  que la funcion f es impar.

funciones inyectivas 

es cuando a diferentes elementos del dominio le corresponden distintos elementos del condominio (rango) y resiprocamente, a distintos elementos del condominio se le asocian a distintos elementos del dominio. tambien se conoce como funcion uno a uno.

funciones suprayectivas

si cualquier elemento del condomino es imagen de por lo menos un elemento del dominio de la funcion.  tambien se le conoce como sobreyectiva.

funciones biyectivas

una funcion es biyectiva si cumple con ser inyectiva y suprayectiva. la regla de correspondencia es biunicuva.